【解答例】円周率は3.05より大きいことを証明せよ

更新：2019/11/29｜公開：2016/12/31 教育・学習

一昨日、「数学的センスは日常生活の中で身に付ける」という記事を公開したところ、記事内で例として挙げている2003年の東大入試問題「円周率は3.05より大きいことを証明せよ」の解答を教えてください、といった問い合わせを結構な数いただきました。

数学の専門的な内容の記事作成の際に、いつも協力いただいている方に連絡したところ、「いくつか解法は考えられるが、年末年始休暇中であまり時間が取れないので、簡単な解法を1つ作成してFAXしておきます」とのことで、おそらく一番簡単な解答をいただきましたので共有させていただきます。

問題解決の考え方（アプローチ）

大学入試問題ですので、高校までで習う範囲で解くこととします。

円周率（以下 $\pi$ と記述する）を何かで近似して、その何かが3.05より大きければ $QED$ （証明終了）となります。何で近似するかで解き方がいくつか考えられますが、円に内接する正多角形を考えるのがすぐ思いつくやり方かと思います。

このアイデアをきちんと整理すると、アプローチは以下のようになります。

①円周率の定義を確認する（⇒必然的に円周の長さが出てくる）

②円周の長さを円に内接する正多角形の周の長さと比較してみようと思いつく

③高校範囲で周の長さが求められる正多角形は何か考える

④絞り込まれた正多角形でいくつか実験してみる

ここまで出れば、手が付けられないということはありません。この手順で実際手を動かしてみます。

まず、円周率とは読んで字のごとく「円周の比率」であり、「円周の直径に対する比率」です。従って、ある円の円周の長さをL、直径（直径の長さ）をRとおくと、

円周率（ $\pi$ ）＝ L/R

となります。

円周率の定義を確認すると、必然的に円周の長さが出てきますので、円周の長さと何かを比較するという発想に自然になります。

円周の長さと円に内接する正多角形の周の長さとの比較実験

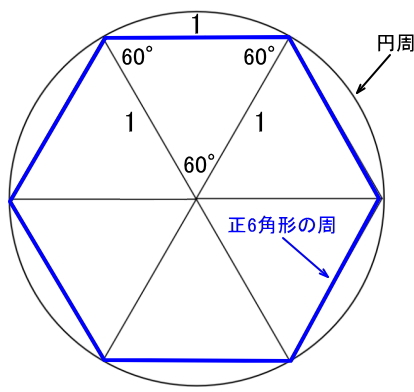
すぐ思いつく（やってみたくなる）のは正6角形かと思います。正6角形は、同じ形・大きさの正三角形（合同な正三角形）に分割できますので、周の長さがすぐに求まります。簡単のために半径1の円とそれに内接する正6角形を考えます。

「円周率（ $\pi$ ）＝円周の長さ/直径」ですので、「円周の長さ＝2 $\pi$ 」となります。上記の通り、「正6角形の周の長さ＝6」ですので、

$2\pi>6$

$\pi>3$

となり、3より大きいというのは出てきますが、「3.05より大きい」が出てきません。円周率は小学校で習いますので、これで解ければ小学校レベルということになりますので、さすがにそう簡単ではないということです。

別の正多角形で実験をするために、どのような正多角形であれば良いか考えます。

まず、正6角形でダメでしたので、それよりも辺が少ないのは除外します。6角形よりも辺の数が多くないと3.05には近づきません。より精度高く円周に近似させなければなりません。

といっても、周の長さ（各辺の長さ）が計算できないとダメですので、6角形よりも辺の数が多ければ何でも良いわけではありません。ここで、辺の長さが計算できる場合というのを詳しく分析する必要があるということが思いつきます。

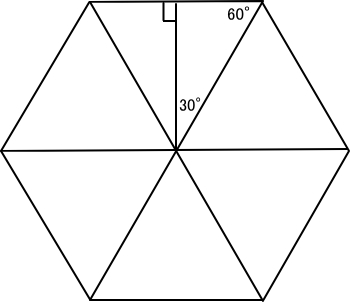
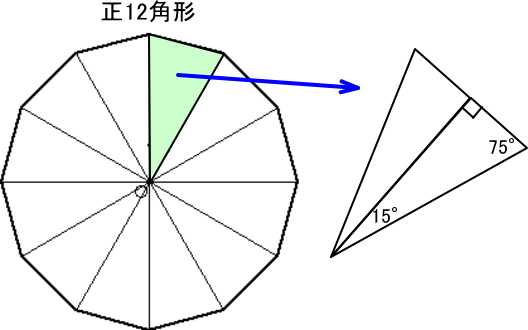
正多角形は、以下のように合同な三角形（同じ形・大きさの三角形）に分割できます。この三角形は二等辺三角形ですので、合同な直角三角形2つに分けられます。（以下は正6角形の例、正6角形以外でも同様）

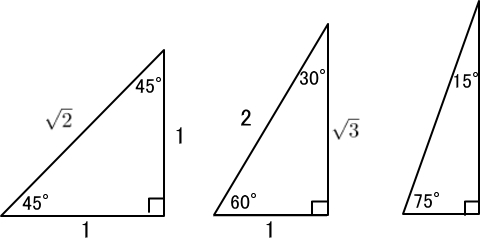
「90度、45度、45度の直角三角形」、「90度、60度、30度の直角三角形」は3辺の長さを知っています（中学校で習います）。また、「90度、75度、15度の直角三角形」も三角関数の加法定理で3辺の長さを求めることができます。（詳しくは後述）

※この3つ以外でも、三角関数表（角度毎の三角関数の近似値を示した表）があれば近似値は求められますが、試験会場で三角関数表は見せてくれませんのでNGです。

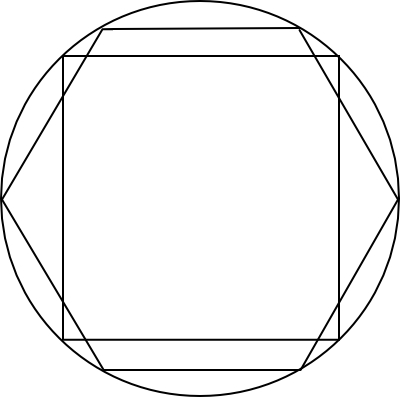
正6角形の場合は、「90度、60度、30度の直角三角形」の場合ですから、これよりも辺の数が多い正多角形にするには「90度、75度、15度の直角三角形」の場合となります。これは正12角形の場合となります。

円に内接する正12角形の周の長さを求めて、円周の長さと比較してみて、それでダメならこのアプローチはダメということになります。しかし、以下に解答を示しますが、正12角形でやれば上手くいきます。

「円周率は3.05より大きいことを証明せよ」の解答例

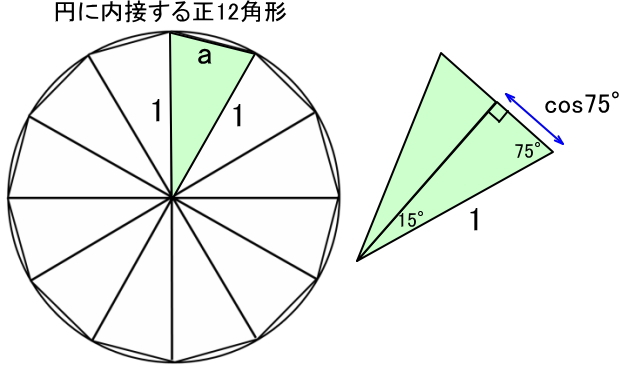
半径1の円に内接する正12角形を考えると、「円周の長さ＞正12角形の周の長さ」となります。半径1であることと円周率の定義から円周の長さは $2\pi$ となり、正12角形の各辺の長さを $a$ とおくと、

$2\pi>12a$

$\pi>6a$

となります。

正12角形は以下のように三角形に分割できますので、 $a=2\cos75^\circ$ となります。

三角関数の加法定理を用いて $a$ を求めます。

$a$

$=2\cos75^\circ$

$=2\cos(30^\circ+45^\circ)$

$=2(\cos30^\circ\cos45^\circ-\sin30^\circ\sin45^\circ)$

参考メモ：三角関数の加法定理

$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$

$\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta$

$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$

$\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$

$\tan x=\sin x/\cos x$ ですので、 $\tan x$ は省略します。

$=2 (\cfrac{\sqrt{3}}{2}\times\cfrac{1}{\sqrt{2}} - \cfrac{1}{2}\times\cfrac{1}{\sqrt{2}})$

$=2 (\cfrac{\sqrt{6}}{4} - \cfrac{\sqrt{2}}{4}})$

$=\cfrac{1}{2} (\sqrt{6} - \sqrt{2})$

$=\cfrac{1}{2} \sqrt{2} (\sqrt{3} - 1)$

$>\cfrac{1}{2} \times 1.414 (1.732 - 1)$

$=\cfrac{1}{2} \times 1.035048$

参考メモ： $\sqrt{2}$ 、 $\sqrt{3}$ の近似値

$\sqrt{2}=1.41421356\ldots$ （一夜一夜に人見頃 / ひとよひとよにひとみごろ）

$\sqrt{3}=1.7320508\ldots$ （人並みにおごれや / ひとなみにおごれや）

※中学校で習いますが、うろ覚えだったとしても、以下のように2乗すれば間違うことはないです。

$(\sqrt{2})^2=2$ 、 $(1.414)^2=1.999396$ なので、 $\sqrt{2}>1.414$ （ $\sqrt{3}$ も同様）

以上をまとめると、

$\pi>6a>6 \times (\cfrac{1}{2} \times 1.035048)=3.105144$

従って、円周率（ $\pi$ ）は、3.105144 より大きいということが証明されましたので、もちろん 3.05 よりも大きい。（ $QED$ ）

※参考メモは、理解促進を目的として記述しています。実際の証明（答案）ではカットしてください。

（参考）数学の問題の解き方

参考までに、大学入試レベルまでにおける数学の問題の基本的な解き方をまとめておきます。（以下を具体的に実施したのが上記です）

①問題解決のアプローチを考える

②考えたアプローチで行けるか実際手を動かして確かめる（トライ＆エラー）

③ダメな場合は別のアプローチを考えて、それを確かめる

④きちんとした解答にまとめる

⑤論理チェックをする（イロジカルな部分がないか、ロジックにジャンプがないか etc.）

※記事作成協力： NPO法人イー・プロフェス　三村彰裕氏（数学に関する主な経歴：早稲田大学大学院理工学研究科数理科学専攻修士課程修了、専門は整数論）

※当サイトではアフィリエイトプログラムを利用しています。

更新日：2019/11/29｜公開日：2016/12/31｜タグ：円周率, 数学

円周率が3.05より大きいことの証明