勉強らしくないのに大きな学びが得られる名門校の名物授業
これまで多くの優秀な人材を社会に送り続けてきた、いわゆる「名門校」には、名物と呼ばれる授業が行われています。伝統的に続けられてきた授業を通して身につけたものは、母校のDNAとなって、卒業生の中にしっかりと根付きます。
どの学校も、先取り学習や最近話題のプログラミングなど目先の教育ではなく、長い人生を力強く生きていく中で役立つ人間力を鍛える授業を展開しています。その背景にある考えや意図を知ることで、名門校の人材育成の極意に触れてみましょう。
灘では、折り紙を使って超難解な数学問題に挑む
灘中学校・高等学校は、最難関大への驚異的な合格率を誇る関西のトップ校
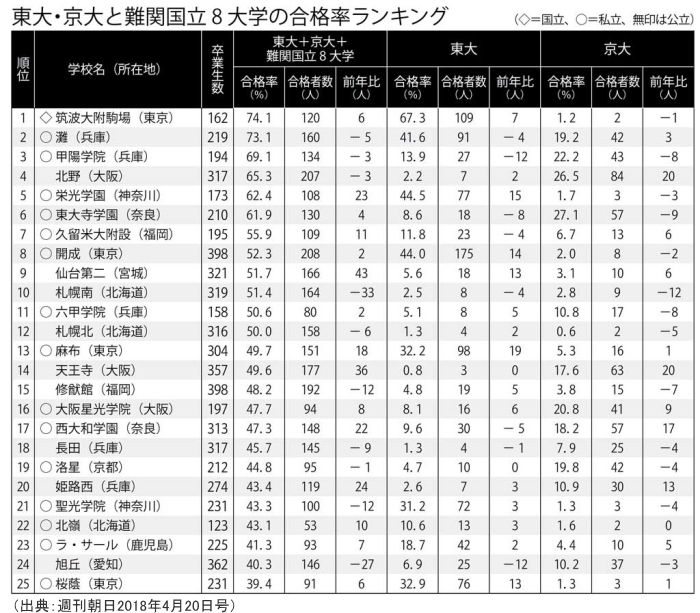
2018年春に発表された「東大・京大に加え、難関とされる国立大8校を加えた10校への、高校別合格率ランキング」を見てみましょう。ここで筑波大附属駒場に続く2位に輝いたのは灘です。
東大合格者数だけを見ると、開成が37年連続トップですが、卒業生の人数に対する国立上位10校への合格率では灘の方が大幅に上回っていることが分かります。
灘から東大に合格したのは91人ですが、そのうち15名は最難関とされる理Ⅲ(医学部)に進んでいます。灘の卒業生数は219人であることを考えても、少数精鋭ぶりが伺えます。
かつて東大合格者数1位と言えば、都立日比谷高校の代名詞でしたが、灘は1968年にその日比谷の壁を初めて打ち破った学校としても知られています。
室町・江戸時代から酒どころとして栄えた、神戸・西宮の沿岸部にある灘五郷地区に灘中学校・高等学校はあります。
灘は、1928年に「菊正宗」、「白鶴」、「桜正宗」といった蔵元が、子弟教育の為に資金を出し合い、菊正宗・白鶴の嘉納家と縁のある教育者であり、講道館柔道の始祖としても知られる嘉納治五郎が創立者となり、開校しました。
中1から高3までの6年間を見通したカリキュラムを組み、各教科の教員で構成された担任団が6年間持ち上がっていく教育システムです。
日本一難しいと言われる算数入試を突破した灘の数学は、中1で中学3年分をカバーするといいます。そして、その後必要になる数学的センスを養うために、中1・中2で幾何を集中的に行うのが特徴です。
土曜日に開講される「土曜講座」では、様々なテーマについて第一人者が講義する
土曜日には正規の授業はなく、代わりに「土曜講座」が開講されています。これは、各界で活躍しているOBを招いて様々な知識を学ぶもので、30年以上の歴史があります。
先輩との接点が持て、生徒にとっては進路選択の上で、また将来社会に出てから非常に役立つものばかりです。
受講の手引きには「関心のある対象についての学習を通じて自分自身を見つめ直し、将来の進路を探ったり、自分の<世界>を広げたりするのに役立ててください。『受動的』に話を聞くという姿勢ではなく、自分なりの問題意識を持って『能動的』に講義に臨むことを期待します」と書かれています。
2018年度は、「AIとは何か、その実態に迫ろう!」「放射線でがんを治す」「日本存続のリスクと発展のオポチュニティ」など29の講座が開かれています。
土曜講座の対象は、中2から高2の生徒で、それぞれ90分の講座を年間最大12コマまで自由に選択することができます。
2017年度の人気講座に「オリガミクス入門」という授業がありました。この授業は、数学で日本最高峰のレベルを誇る灘ならではの名物講座と呼ばれていたものです。
古代ギリシャ以来、定規とコンパスを用いた通常の作図方法では不可能だとされてきたものが、ここ25年ほどで、折り紙を用いることで作図できてしまうことが明らかになりましたが、これを実体験してみようという授業です。
2017年6月に行われた授業では、「任意に与えられた角を三等分することは可能か?」という、ギリシャの3大作図問題の1つである「角の三等分問題」などを扱いました。
このように書くと難解な数学の講義のようですが、グループで助け合い、話し合いながら和気あいあいと取り組んでいく、楽しい講座です。
グループで意見を出し合い課題に取り組む授業は、知的好奇心が刺激される
この日の受講生は中2から高2まで合わせて約100人です。全部で7つの課題が掲載されている小冊子と折り紙を持ち、大教室に集まりました。
担当の河内先生はまず、課題のうち1だけは必ずやること、後は各々好きな課題に取り組むことを説明します。解説までに与えられた1時間は、グループを作ってワイワイ楽しんで取り組むのが河内スタイルです。
課題1で、折り紙を使って作ることができる作図にはどんなものがあるかをそれぞれが確認したら、次の課題へと進んで行きます。
すると、折り紙を折るという作業に加えて計算も必要になってきます。2〜3人のグループの場合、自然に折り紙を折る子、計算をする子、全体を見ながらアドバイスする子と役割分担が生まれます。
講義形式の授業と違い、生徒たちは思い思いにアイデアを出し合いながら、課題を解くことに熱中しています。知的好奇心が強く刺激されていることのあらわれです。
レベルが異なる受講生それぞれに響く内容が用意されている
異学年の生徒を対象にした講座であるため、数学の知識の幅には差がありますが、それぞれのレベルに合った課題を見つけてやれば良いので、参加した生徒は皆自分なりに刺激を受けられるようになっています。
課題に取り組む間、教師は主に見守るのみです。たとえ、あまりの難しさに嫌気がさした様子の生徒がいたとしても、無理強いすることはありません。灘校生の持つ力に信頼を置いているからでもあり、「自由」と「自律」を重んじる灘の校風を表しているとも言えます。
課題は7つ用意されていますが、必ず取り組まなければならないのは課題1だけです。それぞれの課題に付いている問題も、もし難しければ飛ばしながら進んでも構いません。例えば、今回用意された課題7は、次のようなものです。
[課題7]
正方形の折り紙ABCDの対角線を折り、それぞれ対角線AC、BDとする。その交点Fと辺BCとが重なるような折り目を多数折っていくと、放物線が浮かび上がる。このことを、折り紙を実際に折り、確かめなさい。
つまりは、折り紙の中心点を取り、その点と折り紙のある1辺とが重なるように折るということです。角度をずらしながら何度も折っていくと、折り目の中に放物線が現れることが確認できます。解説を聞いて理解するのではなく、手を動かすことで体感させます。
ギリシャ3大作図不可能問題の1つがあっさり証明され、生徒たちは熱狂する
講座開始から1時間、先生による解説の時間が始まります。今回扱うのは、課題6「角の三等分問題」です。定規とコンパスでは作図ができないと1837年に証明されたことが、折り紙を使えば作図できてしまうことを実体験させる課題です。
実際のテキストには、折り紙を折って角の三等分線を作る方法が次のように説明されています。
[折り紙で角の三等分線を作る方法]
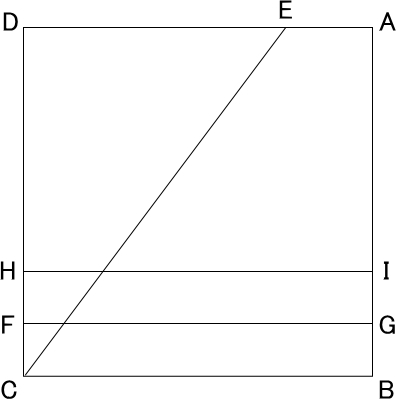
直角あるいは任意の鋭角は、折り紙を使えば三等分にすることができる。正方形の折り紙ABCDの辺DAあるいは辺AB上にとった点Eと、点C・点Bからなる角ECBの三等分線は、以下の方法で織り込むことができる。
手順1:辺BCと平行な折り目を等間隔に2本作る。その折り目を辺BCに近い順にそれぞれ線分FG、線分HIとする。
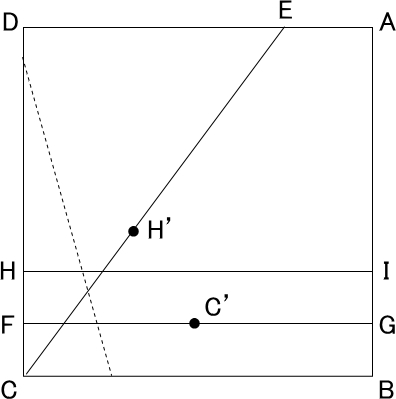
手順2:点Hが直線CE上、点Cが直線FG上にそれぞれくるように合わせて折り目をつける。直線CE上の点を点H’、直線FG上の点を点C’とする。
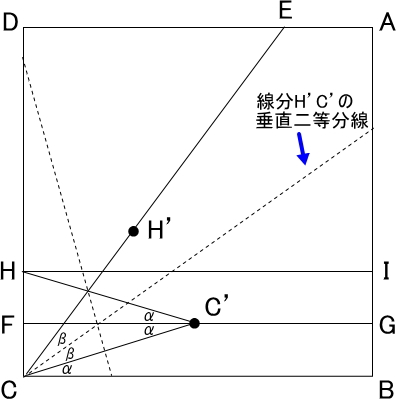
手順3:線分H’ C’の垂直二等分線となる線を折る。この折り目は点Cを通り、点C・点C’とを結んだ線とともに角ECBを三等分していることが確認できる。
説明を読めば、誰でも角の三等分線を作ることはできますが、大切なのは、「この作業でできた線が、なぜ角を三等分しているということになるのか」です。先生の解説は次の通りです。およそ30秒、いたってシンプルなものでした。
「手順1でつけた折り目2つと辺BCは平行だから、角FC’Cと角C’CBは錯角となり等しい。また線分CFと線分 FHの長さは等しいので、角HC’Fと角FC’Cは等しい。手順2でつけた折り目は対称軸となっているため、角HC’C(2α)と角H’CC’(2β)は等しい。」
生徒たちは、かの有名なギリシャ3大作図不可能問題の1つがこのようにあっさりと証明されてしまったことに歓喜の声をあげました。
いわゆる名門校ではしばしば見られますが、知ることへの欲求が人一倍強い灘校生たちと、教師とが一体となって教室の空気が一変する瞬間です。このエネルギーが更なる学びや探求へと繋がって行くのです。
数学の世界の奥深さの一端に触れ、今後の学習のモチベーションを高めるのが目的
文字通り日本1、2番を争う頭脳が集まる灘には、独自でハイレベルな数学のカリキュラムがあります。それに加えてこのような講座を開くのは、現在授業で習っている数学の世界の奥深さを伝えるのが目的です。
折り紙を使ってとっつき易くしているだけで、講座で扱っている課題は高校数学の枠をはるかに超えた難解なもので、受講した生徒の多くが、全てを理解することができないくらいです。
それでも、数学の本質の一端に触れる経験をすることで、現在の数学の授業に意味を見出すきっかけになるのを期待しています。数学というのは、ただ問題を解いていくだけの教科ではないことを伝え、より意欲的に数学に取り組んで欲しいと考えているのです。
高校生になれば、これまで学んできたことと、今回の講座で教わった内容とを具体的に結びつけて数学の世界観を理解することができるでしょうし、中学生ならこれから先の世界を垣間見ることが、勉強のモチベーションになることが期待できます。
その為にも、日々の授業とは異なった角度から数学を楽しんでもらうために、教師は課題選びから当日の講義での言葉遣いまで、あらゆる点に注意を払っています。
数学オリンピックでメダルを取るような生徒も、数学の学習については発展途上の中2の生徒も、それぞれに学びがある授業を目指しています。
特に数学が得意であり、かつ関心が高い生徒を満足させる授業をするのは並大抵のことではありません。
灘では、教師が準備したレベルの高い課題に対し、楽しみながら取り組む生徒の姿があります。学びに貪欲な両者が相互に影響を与え合うことで、この授業に活気が生まれていると言えます。
聖光学院では、レゴブロックを使い数学の概念を理解する授業を実施
本物に接し、自分を高めるための教養講座や体験学習を充実させている
聖光学院中学校高等学校は、1958年に創立されたカトリック系ミッションスクールです。栄光学園、浅野と共に「神奈川御三家」と称される私立の中高一貫男子校で、松任谷由実の「海を見ていた午後」に登場するレストランDolphinからも近い、横浜の山手地区にあります。
近年は東大合格者数ベスト10に毎年名を連ねる進学校としても知られており、2018年度の合格者数は全国7位に輝いています。また、2016年に国際宇宙ステーションに長期滞在した宇宙飛行士・大西卓哉さんは同校の卒業生です。
2017年から文部科学省のSSH(スーパーサイエンスハイスクール)にも指定されるなど、理数系の教育に定評のある同校ですが、それ以外にも特色のある教育プログラムを多く展開しています。
中2では毎週土曜日に「選択芸術講座」を設け、クラシックギターやフルート、陶芸、木工、演劇など11の分野から専門家を招き、それぞれが希望する講座を受講しています。
これは、将来世界に羽ばたく生徒たちが、国際社会でコミュニケーションを取り、自分を表現するためのツールとなることを目指しています。
また、学年の枠を超えた体験型学習講座として「聖光塾」があります。中1対象のものでは、市内に残る里山を、五感をフル稼働させて探索する「里山の自然」や、身近なものを使った様々な実験を行う「おもしろ実験教室」などが開講されています。
それ以外にも「フライフィッシング入門」(中2、中3)、「手話講座」(中1〜高2)、また高1・高2対象の「ジョブシャドウィング」では、夏休みを利用した1日社会人体験として、企業や病院、研究室や建築事務所などの職場体験を行います。
このように、講座の内容は非常にバリエーションに富んでおり、生徒たちの知的好奇心を刺激し、学習意欲の向上に繋がることが期待されています。
数字をブロックに置き換えて理解を促す講座は、グループワークを中心に進める
2017年度に開講されたものの1つに、「レゴブロックで学ぶ数学」という講座がありました。これは、中1の生徒を対象に夏休みの5日間を使い、1回3時間の講義5コマで構成されました。
普通、数学の問題は紙の上と頭の中だけで考えますが、それをブロックに置き換えることで、立体図形や空間などを理解しやすくなります。
また、ブロックのカラーバリエーションを活かして、色で数字などを分類したりするのにも役立つ上、手を動かしてブロックを操作すると記憶に残りやすいというメリットもあります。
初日の授業では、レゴを使って数学の問題に取り組むと分かりやすくなることを実感してもらいます。教室に入ってきた生徒たちは、テキストの冊子と、大量に用意されたカラフルなブロックの中から好きな色を3つ選び、それぞれ6個ずつ取り着席します。
講座を担当するのは、同校の数学科の名塩先生です。先生は、集まった生徒たちに、友達同士でグループを作り、相談しながら課題を進めていくこと、したがって私語も歓迎であることを説明します。
また、冊子に掲載されている一部の課題は解答を配らないので、とことん考えて欲しいということも伝えます。
素因数分解をブロックに置き換えて考えてみる
初日の授業で扱われた2つのテーマのうちの1つは「素因数分解」です。教師はまず、ブロックを素数に置き換えて考えることを説明します。
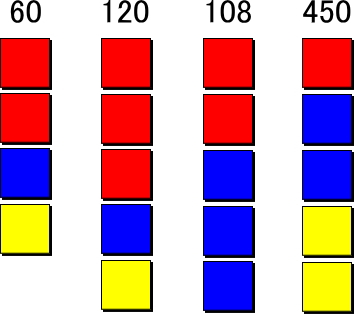
例えば360を素因数分解すると、23×32×5になりますが、それぞれの素数をある色のブロックに置き換えて並べていくよう指示します。
例えば2が赤、3が青、5が黄色のブロックだとしたら、2を3回掛けるので赤のブロックを3個、3は2回掛けるので青を2個、そして5を表す黄色を1個並べます。すなわち「赤・赤・赤・青・青・黄と6つ並んだブロック=360」ということになります。
また、このように分解して並べた6つのブロックの中から選んだものであれば、どれをいくつ掛け合わせても、常に360の約数となることを生徒たちと確認します。
次は、2つの数字の公約数について考えます。120と216の公約数を求めるため、まずはそれぞれを素因数分解し、ブロックで表してみます。
120=23×3×5と216=23×33をそれぞれ先程と同じ色のブロックで置き換えてみると、120は赤・赤・赤・青・黄に、216は赤・赤・赤・青・青・青になります。
2つの数を表したブロックを並べてみて、同じ色と数の組み合わせの部分を抜き出してみると、赤・赤・赤・青になります。この4つを掛け合わせると、2×2×2×3=24となり、120と216の最大公約数が24であることが分かります。
さらに、公倍数についても考えていきます。この場合もまず、それぞれの数をブロックで表します。36と60の公倍数を求める場合は36=22×32(赤・赤・青・青)、60=22×3×5(赤・赤・青・黄)と分解しブロックを並べます。
36と60それぞれの倍数をブロックで表す場合、必ずこのブロック(ex.36の倍数は赤・赤・青・青のブロック)が含まれることになります。
つまり、ある複数の数の公倍数となるためには、それぞれの倍数の条件を満たしている必要があります。36と60の公倍数は180、360、540・・・と続きますが、これらの数字を分解してみると、その中に必ず「赤・赤・青・青」と「赤・赤・青・黄」のブロックが発見できます。
なお最小公倍数は、2つの数字を分解した色別のブロックのうち、個数が最も多いものを組み合わせることによって求められます。36(赤・赤・青・青)と60(赤・赤・青・黄)のブロックから、色ごとに最も数が多いものを取り出すと「赤・赤・青・青・黄」となり、最小公倍数が180であることが分かります。
小学校や塾で、公約数・公倍数については叩き込まれ、迷うことなく求めることができる聖光学院の生徒でも、ブロックを使ってビジュアルで理解をする経験は初めてであり、その仕組みをすっきりと理解することができます。
「すだれ算」の理屈をブロックで解明する
ここまで進んだら、次はメイン課題に取り組みます。テーマは「すだれ算」です。問題文は、「なぜ、すだれ算を行うと複数の数の最大公約数・最小公倍数を求めることができるのかを、ブロックを使いながら解明しなさい。」とあります。
すだれ算と聞いてピンと来ない方も、小学校で習った最大公約数・最小公倍数の求め方のことだと言えば、お分かりになるのではないでしょうか。例えば3つ以上の数字の公約数・公倍数を求める時、すだれ算は以下のようになります。
最大公約数を求める時は、全ての数に共通する約数を使って割り、全てに共通の約数がなくなった時点ですだれ算は終わりです。
一方で最小公倍数を求める時は、最低2つの数字に共通する約数があれば割ることができます。最大公約数を求めるすだれ算よりも長く続き、共通の約数が見つからなくなったら終わりになります。
すだれ算については知っていたとしても、なぜ最小公倍数を求めるすだれ算では、一部の数にだけ共通する約数で割ってしまってもいいのかを説明できる人は多くありません。この理屈を理解することが、この日最大の課題であり、ブロックがその助けになります。
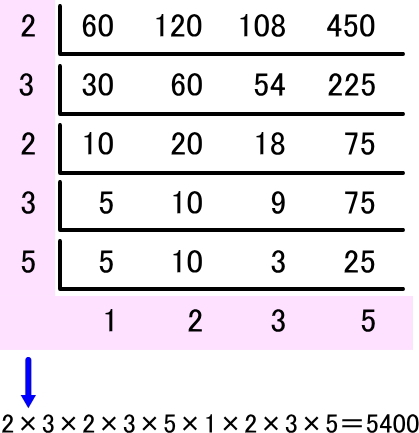
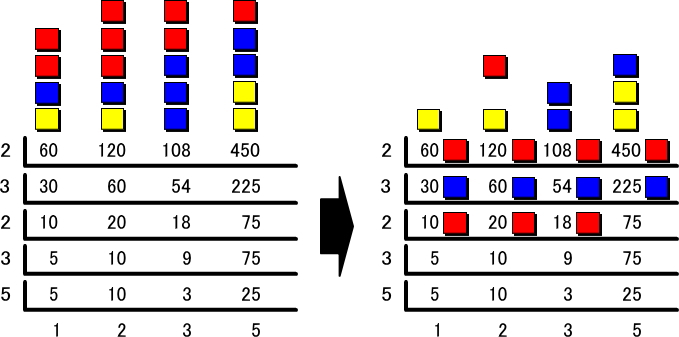
先ほどのすだれ算の結果を、2(赤)、3(青)、5(黄)という3色のブロックに置き換えて考えてみます。まず、4つの数字を素因数分解してブロックで表したものを縦に積み上げたら、すだれ算と同じ要領で、共通の色ブロックを取っていきます。
まずは2で4つの数を割っているので、それぞれのブロックの中から赤のブロックを1つ取ります。次は3が共通する約数なので、青のブロックを1つ取ります。その次は2ですが、これは4つの数のうち3つに共通しているので、赤のブロックを合わせて3つ取ります。
この作業を繰り返していくと、4つの数を表すブロックが、すべてバラバラに分解されることが分かります。すだれ算をあらかじめ書いた紙の上に、分解したブロックを配置していくと一目瞭然です。
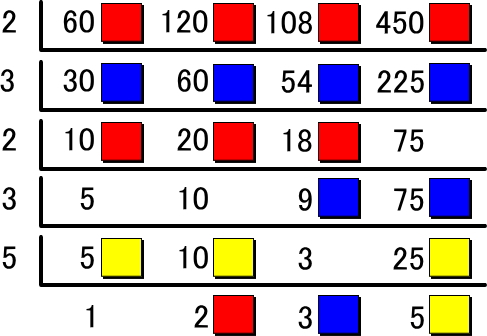
今回のすだれ算では、2(赤)を1番多く使っていたのは120の3個で、3(青)は108で3個使われていました。5(黄)については450で2個と、最も多く使われていました。
各色それぞれの最大値を集めると、赤・赤・赤・青・青・青・黄・黄となりました。数字に直すと23×33×52=5400となり、これがすなわち4つの数の最小公倍数になります。
ブロックを並べて視覚に働きかけることで、難解な数学の概念をすっきりと理解することができるようになります。
授業中には、この課題の解説は行わず、各々が手元のブロックを使って考える時間に使われます。担当の名塩先生曰く、これは「ブロックと参加者との対話」で、これにより自分たちが納得行くまで考えることが大切だと考えています。
この日の授業では約10名の生徒が答えを導き出すことができました。
5日間にわたる講座では他にも、「規則性の発見と数列の和」や「自然数の掛け算と面積図・樹形図」といったテーマを設け、数学オリンピックの過去問や有名なパズルの問題など難問に挑んでいきます。
出発点は数学オリンピックを目指す生徒向けの講座だったが、現在は様々な生徒が集まる
この人気講座の原点は、聖光学院の卒業生でもある名塩先生の学生時代にあります。今でこそ数学オリンピックへの挑戦を後押しし、受賞者も輩出している同校ですが、名塩先生の在学中にはまだ学院内にノウハウが十分ではありませんでした。
数学オリンピックに興味がありながら、他校の生徒のように指導が得られない状況を残念に思ったそうです。そして年月を経て、自らが母校の数学教師となり、この講座を開設することを発案しました。
始まりは数学オリンピックに興味を持った生徒たちの受け皿として始めた講座でしたが、より早い時期から数学好きの生徒の知的好奇心を満たす授業を行うべきだと考え、中1対象の講座として再編したことで、生徒の圧倒的支持を得るようになりました。
受講者が増えるに従って、生徒のレベルにもばらつきが出始めました。初期の頃のような、数学が得意で、数学オリンピックに出たいと希望するような生徒だけが対象ではなくなり、数学に苦手意識があるような生徒にも、理解しやすい授業の進め方を工夫する必要が出てきました。
そこで編み出したのがブロックを使う方法です。4年ほど前から、授業の色々な場面でブロックを用いています。ブロックを使うことで期待しているのは、時間をかけて考える習慣をつけることです。
多くの難問を時間内にこなすことが講座の目的ではないので、テキストの冊子にはあえて解答を掲載していません。
講座をきっかけに数学の世界に興味を持って欲しいという目的もありますが、同時に、じっくりと考える過程で様々なアイデアを生み出す経験をし、そのアイデアを数学ではない他の分野でも発揮して欲しいという狙いもあります。
以前活動していた大輪教授というお笑い芸人をご存知ですか?ホワイトボードを使い、バカデミック数学と題し、様々なものを素因数分解していくネタが人気でした。
サザエさんを素因数分解する場合、まずサザエさんはパーマをかけているので、「パーマ」という素数を除くとただのおっちょこちょいになります。次におっちょこちょいから「失敗」という素数を除くと、失敗をしないおっちょこちょいになります。それはつまり「奇跡」なので、「サザエさん=パーマ×失敗×奇跡」という式が成立するというものです。
これはあくまでお笑いのネタですが、確かに、素因数分解は数学の分野だけのものではないと言えます。
世の中のあらゆる物も、それがどのような要素で構成されているのかを徹底的に分析することで、足りない要素や余分な要素が明らかになり、革新的なモノやアイデアを生み出す力になるかもしれないのです。
桐朋では、なわとび検定を通して、目標に向かい自分なりに工夫し努力する力を養う
自主性と個性を尊重する桐朋で、65年も続く伝統のなわとび授業
東京・国立市にある桐朋中学校・高等学校は創立からまもなく80年を迎える男子校です。幼稚園から高校まで一貫して、生徒一人一人の人格を尊重し、自主性と個性を伸ばす教育で知られる名門校です。
桐朋の名物授業といえばなわとびです。中1から高2まで、3学期の体育の授業ではなわとびをするのが桐朋の冬の伝統になっており、1952年に導入されて以来65年以上も続けられてきました。
しかも特徴はその難易度で、生徒が持っている体育手帳には、現役の体操選手であっても苦戦しそうな難しい技が到達目標として、数多く掲載されています。
桐朋のなわとびの授業では、「単独技」と「規定種目」、そして「自由演技」の3つの項目をそれぞれクリアしていくことを目指します。
「単独技」に挙げられた技は、それぞれ難易度別に点数が設けられています。しかも二重跳びなど簡単なものではなく、二重跳びとあや跳びを組み合わせたものが最低ラインになっているなど、ハードルの高さが伺えます。
「規定種目」は、単独技を4つから7つ組み合わせたものです。レベルは13段階に分かれており、最も簡単とされるレベルなら10点、最高レベルの種目を成功させると700点が与えられますが、ノーミスが合格の条件となっており、非常に厳しい基準をクリアしなければなりません。
「自由演技」は、規定種目のオリジナルアレンジです。同じく4つから7つの単独技の組み合わせになるため、どんな難易度の技を選んだかによって獲得する点数が決まります。検定は先生が行うことになっていますが、低ラインの技の検定は生徒同士で行うこともあります。
生徒たちは、3学期に6〜7回行われるなわとびの授業を通して、なるべく多くの得点を稼ぐことを目指して練習を重ねて行きます。
桐朋のなわとびは、道具を自分流にカスタマイズすることから始まる
桐朋のなわとびは、購買部で持ち手と縄を買い、自分の手や体に馴染むように調整することからスタートします。桐朋生が使っているのは一般的な跳び縄ではありません。竹を切りっぱなしにした持ち手に、ビニールの縄を結びつけて使います。
幅も長さも微妙に違う中から自分に合った竹を選び、4色から選んだ縄も、自分の使いやすい長さにカットします。竹の持ち手部分にビニールテープを巻きつけて補強し、グリップテープの役目も持たせる工夫をしている生徒も見られます。
各々が自分の目標に向かって試行錯誤する授業時間
授業時間には、思い思いに準備運動などのウォーミングアップを済ませたら、体の使い方を先生に教わりつつ、それぞれが自分のクリアすべき目標(技)の練習を始めます。友達同士でチェックしたり褒め合ったりと、桐朋らしく和気あいあいとしています。
同時に担当教師は体育館の隅に机を置き、検定を受けたい生徒の技のチェックを行います。
例えば、規定種目には7つのレベルがあり、高校2年生であれば、下から2つ目の「F難度」の成功を目標に定めています。皆、他の生徒の様子にも注目しており、誰かが高難度の種目に成功すると歓声が響きます。
その反対に、小さなミスでも検定は不合格になってしまうので、悔しい思いをする生徒も数多くいます。上手なクラスメイトに跳び方のコツを聞いたりしながら、自分の体の動きを知り、練習をどのように工夫すれば良いのかを考えるきっかけにもなっています。
コツコツと努力することの大切さは勉強への取り組み姿勢にも繋がる
1952年に開催されたヘルシンキオリンピックの体操の日本代表として出場した金子明友先生は、桐朋で体育を教えていました。
金子先生は、冬になると雪で閉ざされる地域の子供達が、なわとびをすることで必要な運動量を確保できることを知り、それを桐朋の授業に導入したのがきっかけです。
その後、麻縄に代わってビニール製の縄が使われるようになると、様々な技を跳ぶことができるようになり、1960年代には当時の担当教諭により、様々な技が難易度別に分類、整理されました。「規定種目」もこの時誕生するなど、現在の桐朋のなわとび授業の原型となりました。
生徒たちの検定にかける情熱は非常に大きく、授業以外の時間を費やして努力を重ねる生徒も多く見られます。教員たちもそんな生徒の思いに応えるべく、休み時間の臨時検定のリクエストにも対応しています。
3学期が終わる頃のそれぞれの得点を見てみると、かなり大きな開きが発生しています。50点程度でとどまっている子から、上は1000点近く稼いでいる子もいます。ですが、これはそれぞれが生まれつき持っている身体能力の差によるものではありません。
高難度の技が出来ない生徒が得点を積み上げるには、自由演技を活用すれば良いのです。自分ができるレベルの技を複数組み合わせた自由演技で何度も検定を受けることで、高得点が狙える大技が出来ないハンデをカバーすることができるという訳です。
このように、知恵をしぼって工夫する大切さを学ぶことにも繋がっています。
桐朋生にとってのなわとびは、限られた時間の中で、自分に合った練習方法を工夫し、仲間同士でアドバイスをし合い、目標を達成するために必要なものは何かを考えることでもあります。
また、先生たちは、コツコツと努力を重ねて技をマスターした時の達成感も味わって欲しいと願っています。
これは、なわとびに限った話ではなく、大学受験や、この先の人生においても大切な姿勢を学んでいると言えます。現に、なわとびが上手になった生徒は勉学においても努力を惜しまず、良い結果を収めている場合が多いようです。
東大寺学園では、昔から続く読書の時間が、アクティブ・ラーニングの場となる
自由な校風で知られる東大寺は、進度よりも深度を重視した授業を展開する
東大寺学園は、奈良の東大寺を経営母体とする男子校です。制服はおろか、細かい校則も存在しない自由な校風が特徴で、仏教校からイメージする厳格さはありません。
高い進学実績を誇る同校ですが、受験勉強だけの学校生活に陥らず、興味のあるもの、やりたいことを見つけられるような自由な雰囲気が漂っています。
それでも毎年の進学実績は、同じ関西の灘に次ぐ超進学校と呼ぶにふさわしいものです。2018年度も、現役生210名のうち東大に11名、京大には実に33名が合格するなど、関西の中学受験生憧れの学校となっています。
数学では先取り授業を行なっていますが、それ以外の授業では「進度」よりも「深度」を大切に、生徒の知的好奇心を満たす授業を心がけているそうです。その中に、国語の名物授業「読書」もあります。
「読書」の時間の半分近くは脱線トーク、それでも話の核心はブレていない
東大寺学園では、中1で「読書」の時間が設けられています。週1回1時間を使いますが、決められた教科書はないので、取り上げる題材や授業の進め方は担当教諭により様々です。
ある日の授業では、芥川龍之介の『蜘蛛の糸』を扱っていました。前回の授業では先生が本を朗読しており、今回がこの教材で2回目となる授業です。
授業が始まってしばらく経っても、なかなか本題である『蜘蛛の糸』の解説は始まりません。東大寺学園OBでもある担当教諭の中学時代の仲間とのエピソードを面白おかしく話しています。生徒たちは先生の話術に爆笑しながら、目を輝かせて聞いています。
本題に戻ったのは授業も後半に差し掛かった頃です。黒板に一言、「蜘蛛の糸はなぜ断たれたか」と書き、各自がノートに自分の考えを書くように指示しました。
与えられた時間はわずか5分です。先生が机の間を一巡し、それぞれの作業が進んでいることを確認してから、ようやく口を開きました。
「蜘蛛の糸を垂らしたのはお釈迦様だけれど、糸を切ったのもお釈迦様?」これに対して多くの生徒が次々に自分の意見を発言し始めました。授業前半で場の空気があたためられているからか、非常に活発な意見交換が行われます。
先生は適度に口を挟みながら、『蜘蛛の糸』のテーマの1つでもある「エゴイズム」に議論を導いて行きます。
ここで先生は、授業の初めから背中に差し入れてあった2本の長い棒を教卓に出しました。そして、有名な「三尺三寸箸」のエピソードを話します。
ある男が、エンマ様に極楽と地獄の食事風景を見せてもらいました。どちらのテーブルにもご馳走が並んでいるのに、地獄の人たちは痩せこけています。よく見てみると、1メートルはあろうかという長い箸で食べ物をつまむ為、うまく自分の口に運べずにイライラし、挙句の果てには他の人の食べ物を奪おうとして争いまで起こっていました。
一方極楽では、同じく長い箸を使っていますが、つまんだ料理を自分の向かいに座っている人に食べさせてあげ、今度はお返しに向かいの人が料理を食べさせてくれています。つまり、自分さえ良ければいいという考えでは、結局幸せにはなれないという話です。
先生が「極楽と地獄、どっちの食事がいい?楽しく美味しい方がいいと思わない?」と問いかけたところでチャイムが鳴りました。黒板に書いた課題については、各自でまとめるように指示があり、授業は終了です。
読書を楽しむ習慣に繋がるように、様々なアプローチで教材を味わっていく
授業の様子からも分かるように、講義の目的は『蜘蛛の糸』の読解ではありません。東大寺学園に入学して最初の1年間で、本を読む楽しさを知ってもらうことが「読書」の授業の狙いです。このスタイルの授業をもう40年以上続けてきています。
授業を受けた生徒の感想も、「リラックスできる」「楽しみだ」と、学園の狙い通りに本を読むという行為を楽しむ姿勢が身についています。
教材となる書籍選びも慎重に行っています。中1最初の授業では、菊池寛の『形』を取り上げました。
「形」と「中身」がテーマの短編で、「形」ばかりが先行してしまうと「中身」とかけ離れたものになってしまい、やがていつか「形」を失った時に「中身」までも失ってしまうことになるという悲劇を描いています。
担当教諭は、生徒たちに「効率を追求するだけではなく、武道のように『形』を大切にする世界もあることを知って欲しい」という思いがありましたが、同時に形だけにとらわれて欲しくないという願いも伝わるようにと、この作品を選んだと言います。
それ以外にも、音読するとより楽しめる詩を選び、クラスの皆で順番に朗読し、それをテープに録音して聞いてみたり、小説に登場した物に馴染みがなかったら現物を持ち込んで説明したりと、脱線と思われる部分に時間と手間をかけています。
また、先生による朗読も普通には行いません。芝居を演じるような抑揚をつけることで、生徒の関心をそらすことはありません。
教科書は無くツールに頼らない授業だからこそ、教師の真価が問われる
東大寺学園で「読書」の授業を担当するのはベテラン教諭とは限りません。新人であっても同様に、一からレッスンプランを組み立てなければなりません。
教材となる作品を鑑賞するのではなく、その文章を通して生徒に何を伝えたいかを考え、その為に必要な教材を選び、授業を組み立てていく作業は、教師にとっても大切な経験となります。
「読書」の授業の完成度を上げて、生徒たちの知的好奇心を満足させるには、教師自身がどれだけの引き出しを持っているかが鍵となってきます。つまり、教師のレベルが問われているのです。
現在の日本では、2020年の教育改革を見据え、「アクティブ・ラーニング」や「ICT教育(インターネットやデジタルコンテンツ、タブレットなどの情報通信技術を教育で活用すること)」を取り入れることに各学校が躍起になっています。
ですが、教育で本当に重要なのはそういったツールではなく、教師が生徒たちに何を伝えたいのかです。
情報ツールは、教師がレベルの高い授業を展開する手助けとして使うべきですし、教師の力量が高ければ、アクティブ・ラーニングという言葉が登場する前から双方向のやりとりが活発な授業は展開されてきています。
手法は昔のままに、40年以上も前からアクティブ・ラーニングを実践してきた東大寺学園の教育水準がいかに高いかが分かる授業です。